The marble below rolls down a track and around the loop-the-loop of radius R. The marble has mass m and radius r. What minimum height must the marble have to just make it over the loop?

State your answer in terms of the given variables: m, R, r, and g.

Let’s use conservation of energy on this one.

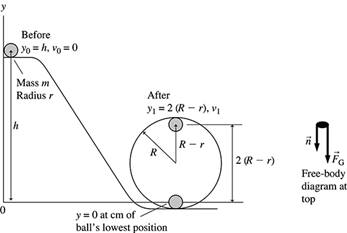
The ball’s center of mass moves in a circle of radius The free-body diagram on the marble at its highest position shows that Newton’s second law for the marble is

The minimum height (h) that the track must have for the marble to make it around the loop-the-loop occurs when the normal force of the track on the marble tends to zero. Then the weight will provide the centripetal acceleration needed for the circular motion.

Since rolling motion requires we have

The conservation of energy equation is

Using the above expressions and the energy equation simplifies to